Page 61 - Saberes y Raíces - Matemáticas 3

L-9

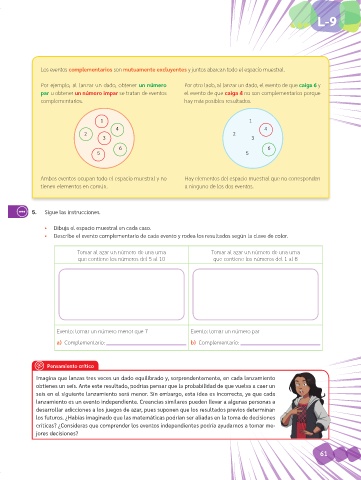
Los eventos complementarios son mutuamente excluyentes y juntos abarcan todo el espacio muestral.

Por ejemplo, al lanzar un dado, obtener un número Por otro lado, al lanzar un dado, el evento de que caiga 6 y
par u obtener un número impar se tratan de eventos el evento de que caiga 4 no son complementarios porque
complementarios. hay más posibles resultados.

1 1
4 4
2 2
3 3
6 6
5 5

Ambos eventos ocupan todo el espacio muestral y no Hay elementos del espacio muestral que no corresponden
tienen elementos en común. a ninguno de los dos eventos.

5. Sigue las instrucciones.

• Dibuja el espacio muestral en cada caso.
• Describe el evento complementario de cada evento y rodea los resultados según la clave de color.

Tomar al azar un número de una urna Tomar al azar un número de una urna
que contiene los números del 5 al 10 que contiene los números del 1 al 8

Evento: tomar un número menor que 7 Evento: tomar un número par
a) Complementario: b) Complementario:

Pensamiento crítico

Imagina que lanzas tres veces un dado equilibrado y, sorprendentemente, en cada lanzamiento
obtienes un seis. Ante este resultado, podrías pensar que la probabilidad de que vuelva a caer un
seis en el siguiente lanzamiento será menor. Sin embargo, esta idea es incorrecta, ya que cada
lanzamiento es un evento independiente. Creencias similares pueden llevar a algunas personas a
desarrollar adicciones a los juegos de azar, pues suponen que los resultados previos determinan
los futuros. ¿Habías imaginado que las matemáticas podrían ser aliadas en la toma de decisiones
críticas? ¿Consideras que comprender los eventos independientes podría ayudarnos a tomar me-
jores decisiones?

61