Page 174 - Saberes y Raíces - Matemáticas 3

e) Tracen un modelo de la figura que se forma si cortan cada cuerpo geométrico de revolución con un plano que con-
tenga el eje de rotación, sin salirse del recuadro.

Del cuerpo generado por B Del cuerpo generado por D Del cuerpo generado por F

• Compartan su trabajo con el grupo. Analicen y comenten si encuentran alguna relación entre los polígonos que
trazaron en el inciso e y el polígono que genera el cuerpo geométrico correspondiente.

¡Miau! Construye las
3. Escribe dentro de cada figura plana la letra que corresponde al cuerpo geométrico de
figuras con papel,
revolución que se genera al girar sobre el eje de rotación.
pégalas en un lápiz y
A – cilindro B – cono C – esfera D – prisma recto gíralas.

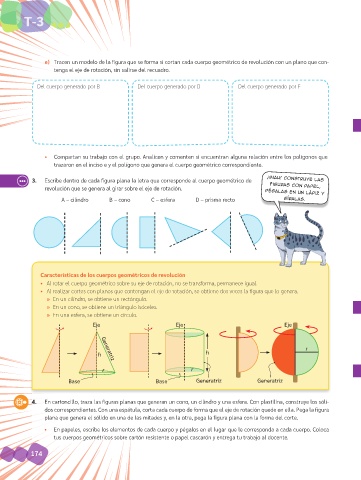
Características de los cuerpos geométricos de revolución
• Al rotar el cuerpo geométrico sobre su eje de rotación, no se transforma, permanece igual.
• Al realizar cortes con planos que contengan el eje de rotación, se obtiene dos veces la figura que lo genera.
» En un cilindro, se obtiene un rectángulo.
» En un cono, se obtiene un triángulo isóceles.
» En una esfera, se obtiene un círculo.
Eje Eje Eje

r
h h
Generatriz
r r

Base Base Generatriz Generatriz

4. En cartoncillo, traza las figuras planas que generan un cono, un cilindro y una esfera. Con plastilina, construye los sóli-
dos correspondientes. Con una espátula, corta cada cuerpo de forma que el eje de rotación quede en ella. Pega la figura
plana que genera el sólido en una de las mitades y, en la otra, pega la figura plana con la forma del corte.
• En papeles, escribe los elementos de cada cuerpo y pégalos en el lugar que le corresponda a cada cuerpo. Coloca
tus cuerpos geométricos sobre cartón resistente o papel cascarón y entrega tu trabajo al docente.

174